Linear & Quadratic Mathematical Models
In the domain of Design of Experiments (DOE), full factorial experiments represent a powerful strategy for exploring the relationship between multiple input factors and one or more output responses. Through a comprehensive investigation of all possible combinations of factor levels, these experiments offer a rich dataset for constructing mathematical models. Two fundamental types of models that emerge from such experiments are linear and quadratic models. These models serve as the backbone for interpreting experimental data, guiding decision-making, and predicting outcomes in various scientific and engineering fields.
Linear Models in Full Factorial Experiments
Linear models are the simplest form of mathematical representation used to describe the relationship between factors and responses in an experiment. They assume a direct, proportional relationship between the inputs and the output. In a full factorial design, a linear model can efficiently identify the main effects of each factor, ignoring the potential interactions and non-linear relationships. The general form of a linear model is expressed as:
Y=β0+β1X1+β2X2+...+βnXn+ϵ
Where:
Y is the response variable.
X1,X2,...,Xn are the input factors.
β0 is the intercept, representing the average response when all factors are at their baseline levels.
β1,β2,...,βn are the coefficients for each factor, indicating the change in response per unit change in the factor.
ϵ represents the random error, capturing the variability in the response not explained by the factors.
Linear models are favored for their simplicity and interpretability, especially when the relationship between factors and response is expected to be straightforward or when exploring a new system with limited prior knowledge.
Quadratic Models for Capturing Complexity
Quadratic models extend beyond linear models by incorporating terms for interactions between factors and quadratic terms for each factor. These models are capable of capturing not only the main effects but also the curvature and interaction effects, providing a more nuanced understanding of the system under study. The general form of a quadratic model is:
Where:
The additional:
terms represent the quadratic effects of each factor, capturing non-linear relationships.
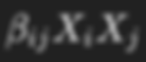
The :
terms account for interactions between factors, indicating how the effect of one factor depends on the level of another.
Quadratic models are particularly valuable in systems where interactions and non-linear effects play significant roles in determining the response. They offer a more comprehensive and accurate representation of the system's behavior, albeit at the cost of increased complexity and the need for more data points to estimate the additional coefficients reliably.
Choosing Between Linear and Quadratic Models
The choice between linear and quadratic models hinges on several factors, including the nature of the system under investigation, the complexity of the relationships, the availability of data, and the goals of the experiment. Linear models are preferred for their simplicity and ease of interpretation, making them suitable for initial explorations or systems where the relationships are predominantly linear. In contrast, quadratic models are chosen when there is evidence of significant interactions and non-linearities, requiring a more detailed and nuanced representation to capture the system's behavior accurately.
Conclusion
Linear and quadratic mathematical models are essential tools derived from full factorial experiments, each offering unique advantages for exploring and understanding complex systems. By accurately representing the relationships between factors and responses, these models enable researchers and practitioners to predict outcomes, optimize processes, and make informed decisions. As the complexity of the systems we aim to understand grows, the thoughtful selection and application of these models become increasingly critical in unlocking new insights and driving progress across diverse scientific and engineering disciplines.