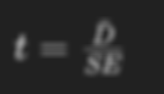In the context of Lean Six Sigma, hypothesis testing plays a crucial role in identifying and validating factors that contribute to process improvement and variation reduction. When dealing with normal data, or data that follows a bell-shaped distribution, selecting the appropriate statistical test is essential for making informed decisions. Among these, parametric tests for normal data stand out for their efficiency and reliability in analyzing the statistical significance of observed changes.

Parametric Tests for Normal Data: An Overview

Parametric tests assume that the data samples come from populations that follow a specific distribution, typically normal. These tests are powerful tools in hypothesis testing because they use the parameters (mean and standard deviation) of the distributions to assess the probability of observing the collected data under the null hypothesis. Within this category, the Paired Samples T-Test holds a significant place, especially in scenarios where the comparison of two means from related samples is required.

Paired Samples T-Test: The Essence

The Paired Samples T-Test, also known as the dependent sample t-test or paired t-test, is a parametric statistical procedure used to compare the means of two related groups. These groups are "paired" because they are related in some way – for instance, measurements taken from the same subjects before and after an intervention, or matched pairs in a case-control study. This test is particularly useful in Lean Six Sigma projects for evaluating the effectiveness of process improvements by comparing performance measures before and after the implementation of changes.

When to Use the Paired Samples T-Test

The Paired Samples T-Test is the tool of choice under specific conditions:

1. The data is continuous (interval/ratio scale).

2. The paired observations are independent of the observations in the other group.

3. The distribution of the differences between pairs is approximately normal.

It's an ideal choice for Lean Six Sigma practitioners aiming to assess the impact of modifications in a controlled environment, ensuring that the observed differences are not due to random chance.

Conducting a Paired Samples T-Test

Performing a Paired Samples T-Test involves several steps, from hypothesis formulation to result interpretation:

1. Formulate Hypotheses: Define the null hypothesis (H0) that there is no difference between the two means, against the alternative hypothesis (H1) that a significant difference exists.

2. Calculate Differences: For each pair, calculate the difference between the two observations.

3. Assess Normality: Ensure the differences follow a normal distribution, which may involve conducting a normality test or visual inspection of plots.

4. Compute Test Statistic: Use the mean of the differences, the standard deviation of the differences, and the number of pairs to calculate the t-statistic.

5. Determine Significance: Compare the calculated t-statistic against the critical value from the t-distribution table or use a p-value to assess the significance of the results.

   
   

Interpretation and Application

A significant result from the Paired Samples T-Test indicates a statistically significant difference between the two paired sets, suggesting that the intervention or process change had a measurable effect. In Lean Six Sigma projects, this insight is invaluable for confirming hypotheses about process improvements and directing efforts towards those changes that yield measurable benefits.

Conclusion

The Paired Samples T-Test is a potent tool in the Lean Six Sigma toolkit for hypothesis testing with normal data, particularly when assessing the impact of improvements on related samples. By rigorously analyzing paired observations, Lean Six Sigma practitioners can make data-driven decisions that enhance process efficiency and product quality, ultimately leading to superior organizational performance.

Paired Samples T-Test real-life scenario

Let's illustrate the Paired Samples T-Test through a real-life scenario in a Lean Six Sigma project aimed at reducing the response time of a customer service department. The department has implemented a new training program for its staff, hoping to improve response times to customer inquiries. To evaluate the effectiveness of this training, we compare the average response times before and after the training for the same group of employees.

For simplicity, let's consider data from 8 employees, showing their average response times (in minutes) before and after the training:

Step 1: Calculate the Mean of the Differences

First, calculate the mean (Dˉ) of the differences (D) between the before and after training times for all employees.

The mean (Dˉ) of the differences (2+3+2+3+4+3+4+3)/8 = 3

Step 2: Calculate the Standard Deviation of the Differences

Next, compute the standard deviation (SD) of these differences to understand how much variability exists in the data.

1. Squared differences (D-Dˉ^2) for each pair:

(2−3)^2=1

(3−3)^2=0

(2−3)^2=1

(3−3)^2=0

(4−3)^2=1

(3−3)^2=0

(4−3)^2=1

(3−3)^2=0​

1. Sum of squared differences:

1+0+1+0+1+0+1+0=4

1. Variance calculation (n−1=7):

Variance=4/7​

1. Standard Deviation (SD):

Step 3: Compute the T-Statistic

First, we calculate the SE:

SE ≈0.267

Then, The formula for the t-statistic in a paired samples t-test is:

With:

SE ≈0.267 Dˉ = 3 (Previously calculated)

So we get, t≈11.22

Step 4: Determine the Degrees of Freedom

The degrees of freedom (df) for this test is n−1.

df=8−1=7

With 7 degrees of freedom, we can now look up the critical t-value in a t-table

Step 5: Find the Critical Value or P-Value

We'll consider an Alpha of 0.05

Using the calculated t-statistic and the degrees of freedom, we find the critical value or p-value from the t-distribution table to determine the significance of our results.

For an alpha level of 0.05 (which for a two-tailed test effectively becomes 0.025 for each tail)

For an alpha level of 0.05 and 7 degrees of freedom, the critical t-value from the t-distribution is approximately 2.365. This means that for a two-tailed test, if the calculated t-statistic exceeds 2.365 (in absolute value), the difference is considered statistically significant at the 0.05 significance level. Our calculated t-statistic of approximately 11.225 far exceeds this threshold, confirming the significance of our findings.

Conclusion

The statistical analysis suggests that the training program significantly reduced the average response time of the customer service employees. This demonstrates the effectiveness of the training intervention in improving operational performance in the customer service department, aligning with the Lean Six Sigma objective of enhancing process efficiency.